Morten Pettersson er adjunkt ved UCL Erhvervsakademi og Professionshøjskole, Center for Anvendt Skoleforskning, og tilknyttet Læremiddel.dk. I Læremiddel.dk har han tidligere været involveret i et projektet ’Adaptive Læremidler’ og ’Kvalitet i dansk og matematik’. I øjeblikket arbejder han med en ny læsevaneundersøgelse kaldet Børn og unges læsning 2021 samt en ny international undersøgelse kaldet ICILS Teacher Panel Study.
Del 3: Beregn statistisk usikkerhed for kategoriske variable
Lær at udregne statistisk usikkerhed og fejlmargin for kategoriske variable i dine stikprøver, hvilket hjælper med at vurdere, hvor præcise dine resultater er i forhold til den større population.
Korrekt citering af denne artikel efter APA-systemet (American Psychological Association System, 7th Edition):
Pettersson, M. (2024). Del 3: Beregn statistisk usikkerhed for kategoriske variable. Lokaliseret på: /viden-og-vaerktoejer/statistisk-analyse-af-kvantitative-data/del-3-beregn-statistisk-usikkerhed-for-kategoriske-variable/
Når man udfører kvantitative undersøgelser, er en central overvejelse, hvorvidt de indsamlede data er dækkende for den population, man ønsker at udtale sig om. Kort fortalt: Kan vores resultater generaliseres, og i så fald med hvilken usikkerhed? Populationen er den samlede gruppe af enheder, man ønsker at udtale sig om (Agresti & Finlay, 2009, s. 4). Den kan variere i både størrelse og omfang – fra alle elever i 5. klasse i Danmark til 5. klasseelever i en enkelt kommune eller på en specifik skole.
Hvis dataene kommer fra en populationsundersøgelse, hvor man har forsøgt at indsamle data fra alle enheder i populationen, kan man som udgangspunkt antage at dataene er dækkende. Det gælder dog kun, hvis data er indsamlet fra langt størstedelen af populationen. Selv i sådan tilfælde kan det være nødvendigt at udføre en bortfaldsanalyse for at sikre, at de, der har svaret, ligner populationen som helhed med hensyn til vigtige karakteristika (se mere om bortfaldsanalyse i Hansen et al., 2015, s. 196-197)[1]. I populationsundersøgelser, som oftest kun er mulige, men også det bedste valg, i små populationer (fx 5. klasserne på en specifik skole), er det ikke relevant at overveje beregning af statistisk usikkerhed.
Hvis dataene stammer fra en bekvemmelighedsstikprøve – hvor man kun har forsøgt at indsamle data fra en subgruppe af populationen, typisk dem, der er nemmest at få fat på, uden at sikre at hver enhed har haft en kendt chance for at blive udvalgt – kan resultaterne ikke generaliseres til en større population. Disse stikprøver afspejler kun de undersøgte enheder, og derfor kan statistisk usikkerhed eller en fejlmargin i forhold til populationen ikke beregnes på en meningsfuld måde.
Men hvis data derimod er indsamlet med en sandsynlighedsbaseret stikprøve, dvs. en subgruppe udvalgt fra populationen ved lodtrækning (Agresti & Finlay, 2009, s. 15), er der en naturlig statistisk usikkerhed forbundet med resultaterne. Denne usikkerhed kan beregnes som en fejlmargin, og giver indsigt i hvor meget stikprøveresultaterne potentielt kan afvige fra den faktiske værdi i hele populationen. Denne type analyse kaldes inferentiel statistik, da man her forsøger at forudsige resultatet i en større population baseret på data fra en stikprøve (Agresti & Finlay 2009, s. 7). Dette adskiller sig fra deskriptiv statistik, som kun beskæftiger sig med at beskrive data i den konkrete stikprøve, man har til rådighed, uden at generalisere til en bredere population.
Ved en sandsynlighedsbaseret udvælgelse er udvælgelsen ikke foregået uden en metode: hver enhed i populationen har haft en kendt sandsynlighed for at blive udvalgt (Thomsen & Risbjerg, 2020, s. 353). Det er netop, fordi hver enhed har haft en kendt chance for at blive udvalgt ved lodtrækning, at man ved hjælp af statistiske formler kan beregne usikkerheden på resultatet. Den mest enkle metode til denne udvælgelse er simpel tilfældig udvælgelse, hvor alle enheder har lige stor chance for at indgå i stikprøven. Den statistiske usikkerhed opstår, fordi analyserne baserer sig på data fra et lille og tilfældigt udsnit af en større population, og derfor ikke nødvendigvis præcist afspejler billedet i hele populationen. Enhver stikprøve er kun én blandt mange mulige, man kunne have fået ved lodtrækning, og hver vil sandsynligvis give lidt forskellige resultater i forhold til, hvordan det ser ud i hele populationen.
Fordelene ved denne udvælgelsesmetode er dog helt klare. Som nævnt gør den det muligt at beregne, hvor meget resultatet i stikprøven kan afvige fra det faktiske resultat i populationen. Det er en stor fordel, fordi vi kan kvantificere, hvor præcise vores resultat er i forhold til populationen. Dog kræver det en høj svarprocent for, at stikprøven kan betragtes som tilfældigt udvalgt og for, at den statistiske usikkerhed kan beregnes meningsfuldt – minimum 50 %, men helst over 70 % (Hansen et al. 2015, s. 89). Desuden gælder, at jo større stikprøven er, desto mere sandsynligt er det, at den præcist afspejler populationen.
[1] Dette gælder dog også i stikprøveundersøgelser.
Eksempel
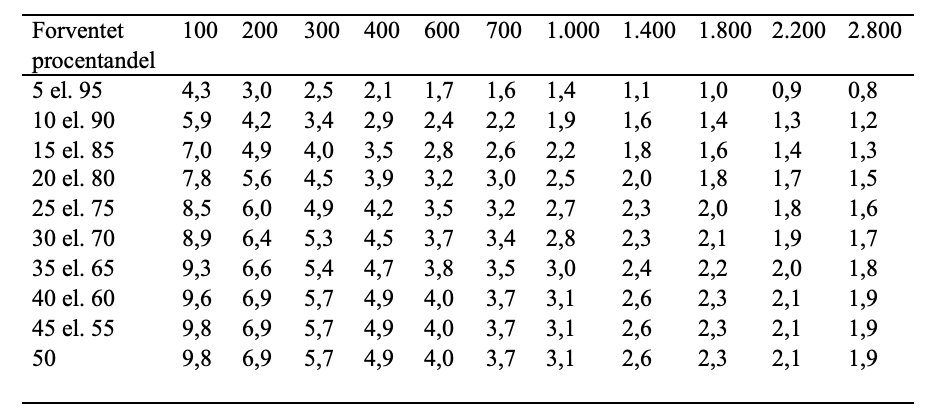
For at illustrere hvad statistisk usikkerhed og en beregnet fejlmargin betyder i praksis, lad os fortsætte vores eksempel: Forestil dig, at vi i vores undersøgelse om køn og holdninger blandt danske borgere over 18 år har fundet, at 51 % af de adspurgte erklærer sig enige, hvor stikprøven i dette tankeeksperiment er en simpelt tilfældigt udvalgt gruppe på 500 personer. Hvis denne måling har en fejlmargin på +/- 4 procentpoint, betyder det, at den holdning i populationen sandsynligvis ligger et sted mellem 47 % og 55 %.
Din stikprøveandel +/- fejlmargin angiver et såkaldt 95 % konfidensinterval. Det betyder, at hvis vi gentog undersøgelsen mange gange, fx 100 gange, og hver gang beregnede dette interval, ville vi i 95 af tilfældene forvente, at intervallet indeholdt den sande andel i populationen (Agresti & Finlay, 2009, s. 115).
Vi kan med andre ord ikke sige, at andelen af enige i populationen præcist er 51 % – det er vores bedste bud. Men vi kan være ret sikre på, at den falder inden for dette interval.
Fejlmarginen er direkte konsekvens af, at stikprøven kun er en tilfældig delmængde af den samlede population. Jo større stikprøven er, desto mindre bliver fejlmarginen, og dermed bliver vores estimerede bud på andelen, der er enige, mere præcist. Hvis stikprøven var fire gange så stor, kunne fejlmarginen reduceres til +/- 2 procentpoint, hvilket ville give et endnu mere præcist bud på den reelle enighed.
Læs mere om beregning af statistisk usikkerhed
Fejlmarginen for en kategorisk variabel kan beregnes med følgende formel (Agresti & Finlay, 2009, s. 110-112):
Hvor:
• 1,96 er en såkaldt z-værdi, som man bruger til at beregne fejlmarginen i et 95% konfidensinterval
• p er den observerede procentandel i stikprøven og udtrykt som et decimaltal (fx 0,5 for 50 %)
• n er stikprøvens størrelse.
Formlen beregner hvor meget stikprøveresultaterne kan afvige fra den sande andel i populationen med 95 % sandsynlighed. Med andre ord, hvis vi gentog undersøgelsen mange gange, kunne vi forvente, at intervallet dannet af stikprøveresultatet plus/minus fejlmarginen indeholder den sande andel i 95 ud af 100 tilfælde.
Størrelsen på fejlmarginen for kategoriske data afhænger af stikprøvens størrelse samt den procentandel, vi ønsker at udregne usikkerheden for. Fejlmarginen falder naturligvis, når stikprøven bliver større, men den afhænger også af resultatets størrelse. Faktisk er der større usikkerhed forbundet med et resultat på 50 % end på 10 % eller 90 %. Det skyldes, at en procentandel på 50 % repræsenterer et punkt, hvor der er størst mulig variation på udfaldet, fordi populationen er lige opdelt. Ved 50 % er det lige så sandsynligt, at en enhed falder i den ene eller den anden kategori, hvilket gør resultatet mere følsomt for forskelle i stikprøver. Ved 10 % eller 90 % er fordelingen mere entydig, mindre påvirkelig af små forskelle i stikprøver, og derfor usikkerheden lavere.
Nedenstående tabel viser, hvordan fejlmarginen afhænger af stikprøvestørrelse og forventet svarfordeling (fra Hansen et al., 2015, s. 73):
Tabel 2. Sammenhæng mellem stikprøvestørrelse, forventet svarfordeling og fejlmargin.
Excel-instruktion: Sådan beregner du statistisk usikkerhed for kategoriske variable
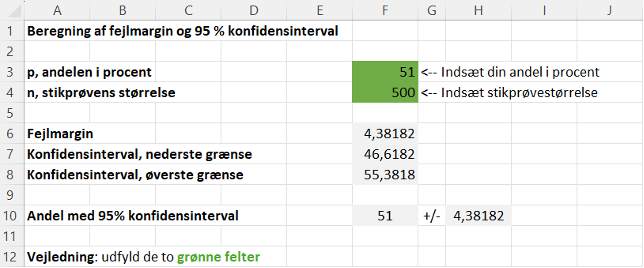
At beregne statistisk usikkerhed på dine stikprøveresultater kan være komplekst på grund af de nødvendige formler. Men ved hjælp af det vedhæftede Excel-ark er det ligetil. Her forklarer vi, hvilke informationer du skal indtaste, og hvordan du skal forstå de resultater, der bliver beregnet (se også Figur 2).
Ark til beregning af statistisk usikkerhed her
Her er de grundlæggende trin:
- Indsæt resultat og stikprøvestørrelse: I feltet ud for “Andelen i procent” indsætter du den stikprøveandel, du ønsker at beregne usikkerheden for (fx procent enige). I feltet ud for “Stikprøvens størrelse” angiver du antallet af enheder i din stikprøve.
- Forstå fejlmargin og konfidensinterval: På baggrund af dine input returneres en fejlmargin på dit stikprøveresultat.
Hvis din stikprøveandel fx er 51 %, og stikprøvestørrelsen er 500, vil fejlmarginen være ca. 4 procentpoint. Det betyder, at den faktiske procent i hele populationen, som din stikprøve repræsenterer, med 95 % sikkerhed ligger mellem ca. 47 % og 55 %. Din stikprøveandel +/- fejlmargin angiver et såkaldt 95 % konfidensinterval. Det betyder, at hvis vi gentog undersøgelsen mange gange, fx 100 gange, ville vi i 95 af tilfældene forvente, at det beregnede interval indeholdt den sande andel i populationen.
Figur 2. Excelark til udregning af statistisk usikkerhed.
Flere artikler i denne serie
Introduktion til Statistisk analyse af kvantitative data
Del 1: Begrebsgymnastik: Variabel, enheder og værdier
Del 2.a: Analyse af én variabel: Kategorisk variabel
Del 2.b: Analyse af én variabel: Metrisk variabel
Del 4: Analyse af to variable: Krydstabel
Litteratur
Aagerup, L. C. (2015). Pædagogens undersøgelsesmetoder. Hans Reitzels Forlag.
Aagerup, L. C., & Willaa, K. C. W. (2016). Lærerens undersøgelsesmetoder. Hans Reitzels Forlag.
Agresti, A. (2018). Statistical methods for the social sciences (5. udgave). London: Pearson Education Limited.
Agresti, A., & Finlay, B. (2009). Statistical methods for the social sciences (4. udgave). New Jersey: Pearson Education.
Hansen, K. M. & Hansen, S. W. (2020). Univariat analyse. Side 368-392 i K. M. Hansen, L. B. Andersen & S. W. Hansen (red.) Metoder i statskundskab (3. udg.). København: Hans Reitzels Forlag.
Hansen, N.-H. M., Marckmann, B., Nørregård-Nielsen, E., Rosenmeier, S. L., & Østergaard, J. (2015). Spørgeskemaer i virkeligheden. Frederiksberg C: Samfundslitteratur.
Thomsen, S. R., & Hansen, K. M. (2020). Stikprøveudvælgelse. Side 352-367 i K. M. Hansen, L. B. Andersen & S. W. Hansen (red.) Metoder i statskundskab (3. udg.). København: Hans Reitzels Forlag.
