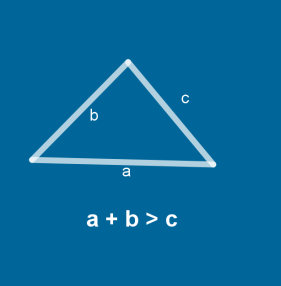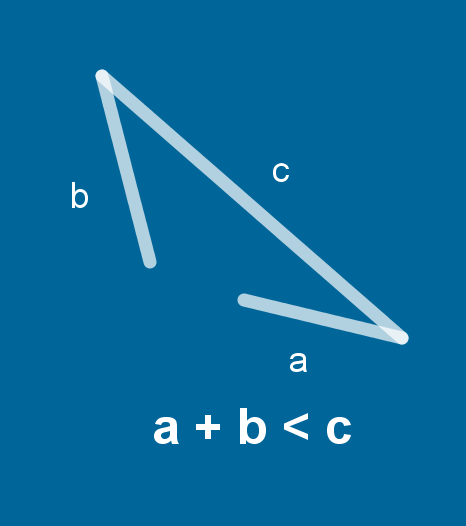Artikel

Computationel tankegang i matematik – nye modaliteter og nye repræsentationer

Med et udgangspunkt i matematikfaget og den del af teknologiforståelse, der har tydelige historiske snitflader med matematikfaget, bliver den undersøgelse måske mere en undersøgelse af nye repræsentationsformer og oversættelser mellem disse.

Hvor multimodaliteten beskriver forskellige formidlingsveje, vil de multible matematiske repræsentationer være måder at repræsentere og dermed give adgang til et givent matematisk fænomen.

   

Et tænkt eksempel kan her være en trekant. Her vil en multimodal beskrivelse af trekant måske inddrage en video, der med animationer viser, hvorfor det gælder, at en trekant altid vil og skal have, at summen af to sidestykker er længere end det tredje uanset, hvilke to linjestykker man vælger [figur til venstre]. Dette vil kunne efterfølges af et link til en øvelse i et dynamisk geometriprogram, hvor man selv kan afprøve påstanden. Formidlingsvejene vil her være at se og høre forskellige repræsentationer af trekant efterfulgt af manipulation af trekant. Her bliver overlappet til matematiske repræsentationer også tydeligt, da der arbejdes med overgangen mellem algebraiske beskrivelser og geometriske konstruktioner [figur til venstre].

Dette er ikke en trekant

Man kan ikke holde det matematiske begreb trekant i hånden, men man kan klippe eller tegne eksempler på trekanter, konstruerer dem og beskrive dem. Hverken den matematiske beskrivelse eller den eksemplariske udklippede trekant er andet end repræsentationer af trekant; de er ikke trekant. Det abstraktionsniveau er centralt i matematikfaget, lige som overgangen mellem de forskellige repræsentationer er der, hvor eleverne fåor blik for de abstrakte matematiske objekter (Duval, 2006).

Nye formidlingsveje af ’trekant’

Med introduktionen af teknologiforståelse som en del af matematikfaget vil ’trekant’ kunne blive beskrevet via nye repræsentationer og overgange, der på hver deres måde giver mere indsigt i trekant, ligesom der vil komme nye formidlingsveje af ’trekant’. En computationel tænkning om trekant vil ganske enkelt være en anden end en euklidisk tænkning. Dette er dog ikke nødvendigvis det, der sker.

Teknologiforståelse åbner nye veje

En del af de forløb der lige nu afprøves i grundskolens matematikundervisning tager udgangspunkt i kendte tilgange til skolematematikken. Det kan fx være at arbejde med at bygge en lommeregner i blogprogrammering eller lave et sænke slagskibs-spil for at forstå koordinatsystemet. Eksemplerne viser, hvordan arbejdet med teknologiforståelse kan åbne nye formidlingsveje, hvor eleven ikke længere er bruger af et læringsmiddel læremiddel udviklet til dem, men skal forstå lommeregneren eller spillet  nok til selv at kunne konstruerer det.

Uden for de traditionelle fagrammer sker der også en del afprøvninger, der mere har et udgangspunkt i det 21. århundredes kompetencer (http://info.21skills.dk/). Det ses bl.a. i CodingClass fra it brancheforeningen og C.R.A.F.T.-konkurrencen fra Styrelsen for it og læring. Her er læringsudbyttet koblet på et overordnet kompetencebegreb og ikke som sådan med det fælles fagdomæne som computering og algoritmetik har med matematik. Ligesom koblingerne mellem computationel tankegang, -problemløsning, -ræsonnement og -modellering ikke kobles på de matematiske ditto kompetencer.

Ved at acceptere slægtskabet mellem matematikken og computervidenskaben vil man finde, at meget at det arbejde, der sker både videnskabeligt og inden for industrien, indeholder et væld af eksempler på konkret matematik, der både vil give andre repræsentationer og formidlingsveje end de ovenstående eksempler (Knuth, 1989).

Forståelige repræsentationer af objekter

Et af de områder er, hvordan man grafisk skriver til en skærm. Det første eksempel på den måde at tænke computeranimation kan ses i en ’making of’-film fra 1972. Det er et arbejde, der stadig pågår og har betydning inden for så forskellige domæner som underholdning i spil og film, repræsentationer af hjerner efter MRI-scanninger og visning af stjernefødsler i stjernetåger ud fra astronomiske målinger samt mange andre områder.

Det er et område, der bygger på antagelsen om, at alle geometrier kan beskrives ud fra punkter og linjer. Fladerne mellem linjerne kan man give forskellige overflader og lys til at skabe en for mennesker forståelig og acceptabel repræsentation at et givent objekt, som fx hånden herunder.

Ved at lave en didaktisk transpositionering af dette domæne ned til grundskolen, vil man kunne finde andre veje til at arbejde med forståelse af matematiske objekter og transformationer, der udfordrer elevers computationelle såvel som matematiske tankegang, repræsentations- samt modelleringskompetence (Chevallard, 1988).

En almindelig computerskærm består af et net af små kvadrater, skærmopløsningen fortæller, hvor mange af de små kvadrater, der er. Computeren skriver til skærmen ved at køre sit program, der svarer, på hvilken farve det givne pixel skal farves – et pixel ad gangen.

I et mindre projekt blev der forsøgt at arbejde med skærmgrafik ud fra, at de programmer man skriver, skal kunne svare på, hvordan hver enkelt pixel skal farves. Det gav nye måder at repræsentere trekant og nye abstraktioner og overgange at forstå.

Så lige som Papert (1999) gav veje til at arbejde med geometriske objekter tegnet ud fra en robots perspektiv gennem programmeringssproget LOGO og programmeringen af en skildpadderobot, vil grafik-programmeringen give andre veje.

Tidligere blev trekanten beskrevet ud fra krav til sidelængdernes interne forhold i planen. Den måde at beskrive en trekant hjælper dog ikke, hvis vi skal kunne repræsentere en trekant som et program, der fortæller, hvilke pixels der skal farves på en skærm.

I den begyndende forståelse af grafik-programmeringen vil perspektivet være et mængdelæreprincip, hvor en trekants linjer beskrives som funktionsforskrifter, og hvor mængderne defineres som et sæt af uligheder.

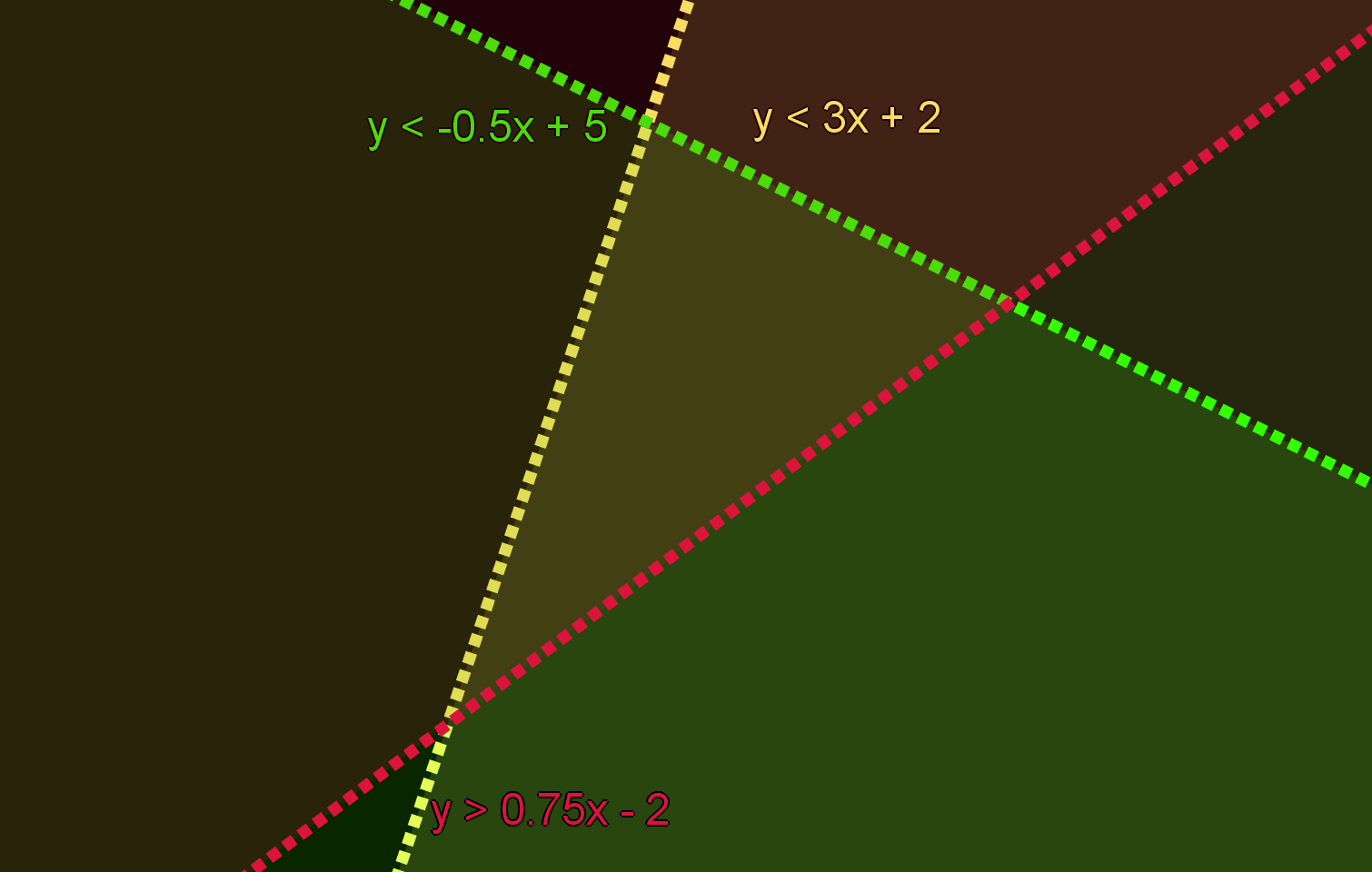
Her kan man beskrive en trekant som det rum, der er omkredset af tre funktioner, hvorom det gælder, at ingen af funktionerne har samme hældningstal (se figur 3).

I et mængdelære-perspektiv bliver trekanten til mængden af punkter i et koordinatsystem, der er beskrevet ved hjælp af 3 lineære uligheder, hvis grænser ikke ligger parallelt og er defineret på en sådan måde, at en ulighed altid må og skal afgrænse en mængde af punkter, der også indeholder punkter fra de to øvrige uligheders fællesmængde (Se Figur 4).

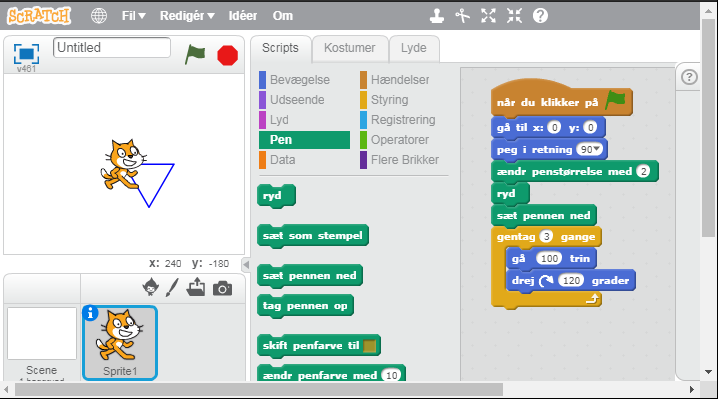
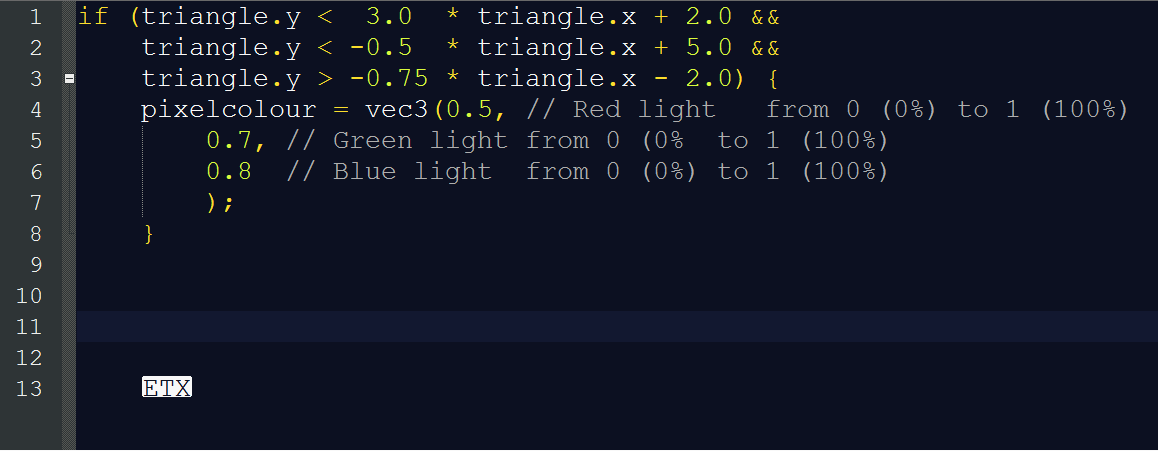
Den endelige programmering ville kunne se ud som nedenfor.

Tilføjelsen af nye modaliteter og oversættelsen mellem nye repræsentationsformer giver på den måde ikke blot flere måder at repræsentere det abstrakte objekt trekant på, men også nye veje til at arbejde undersøgende i et responsivt miljø med forståelse af ’trekant’ samt sammenhængen mellem forskellige matematiske områders måder at beskrive og repræsentere på. Ligeledes vil der sidenhen kunne manipuleres med tid og støj for at give den abstrakte geometri overflader og bevægelser, der giverså vi ser grafiske udtryk, der ligner levende objekter eller smukke stjernetåger.